フィボナッチ比率(Fibonacci ratio)

初項 1，第２項 1として、隣り合う項の和が次の項の値となるような数列をフィボナッチ数列という。

• 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,…………
• a(n+2) = a(n) + a(n+1)

この数列に現れる任意の二つの数字の比がフィボナッチ比率(fibonacci ratio)である。各項の数値はフィボナッチ数と呼ばれることがある。例えば、

• 21/89 = 0.236
• 55/144 = 0.382
• 144/233 = 0.618
• 55/34 = 1.618
• 233/89 = 2.618
• 610/144 = 4.236

数列の初期段階においては顕著ではないが、一般に隣り合う項の比は常に0.618（またはその逆数の1.618）となる。これが黄金分割比と呼ばれる不思議な性質を持った数字で、古来より建築やデザインなどの分野で応用された例があり、宇宙で見られる現象（星雲の渦巻きなど）に黄金分割比を使って説明できる法則が知られている。さらに、木の枝別れがフィボナッチ数列に従うという事例も発見されている。ここから、無秩序とも思える自然現象も実は、その現象がそうなるように何らかの法則に支配されたためという考え方が生まれておかしくない。これが発展して、自然現象はフィボナッチで説明できる。ならば、一見、気ままで不規則と見られる相場の値動きにもフィボナッチの法則が適用できるのではないか？　このような観点から構築された理論がエリオット波動理論である。

[実例]

原則論として相場の先行きは誰にもわからない。しかし、相場がどこまで行き着くか、その見当をつけないことには相場に勝てない。このとき、ひとはできるだけ合理的な説明を試みて相場を予測しようとするはず。その説明によく用いられる手法がフィボナッチ比率だ。

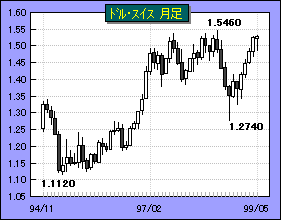
左図はドル・スイスフラン相場の月足である。
1.1120から 1.5460まで上昇した相場が短期間に 1.2740まで下落した。このときの下落幅 0.2720はそれまでの上昇幅 0.4340のほぼ 61.8%。正確には 0.2682だけ下落すれば見事だったが、約 2700ポイント（＝0.2700）という大きな変動をした相場の流れで計算値とわずか 0.0038の差は誤差ともいえない。完璧な修正、100点満点だったといってよいだろう。相場の戻りは黄金分割比に従う（ことがある）という合理的な説明が成り立ったケースだ。
（当サイトのこちらのページにもフィボナッチに関する、相場における興味深い話題がある）